Answer:
A. -0.003
B. 0.02
Step-by-step explanation:
Step 1: identify the given parameters
Giving the following parameters
Wing area (S)= 1.5 m²
Wing chord (C) = 0.45 m
Velocity (V) = 100 m/s
moment about center of gravity(Mcg) = -12.4 N-m
at another angle of attack, L = 3675 N and Mcg = 20.67 N-m
Step 2: calculate the value of the moment coefficient about the aerodynamic center (Cmcg)
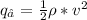
 = 6125 N/m²
= 6125 N/m²
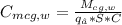
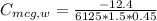 = -0.003
= -0.003
 at zero lift
at zero lift
Step 3: calculate coefficient of lift
Cl = L/q*s
Cl = 3675/6125*1.5 = 0.4
Step 4: calculate the location of the aerodynamic center
New moment coefficient about the aerodynamic center (Cmcg):
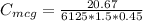 = 0.005
= 0.005
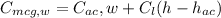
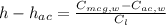
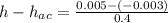 =0.02
=0.02
the location of the aerodynamic center = 0.02