Answer: The required ordered pair (p, q) is (-7, -12).
Step-by-step explanation: Given that (x+2)(x-1) divides the following polynomial f(x) :
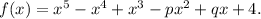
We are to find the ordered pair (p,q).
We have the following theorem :
Factor theorem : If (x-a) divides a polynomial h(x), then h(a) = 0.
According to the given information, we can say that (x+2) divides f(x). So, we get
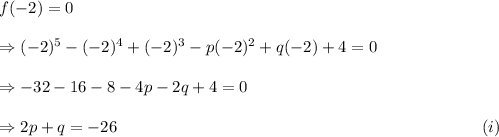
Also, (x-1) is a factor of f(x). So,
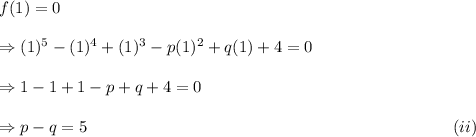
Adding equations (i) and (ii), we get
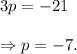
From equation (ii), we get
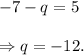
Thus, the required ordered pair (p, q) is (-7, -12).