Question

If $x^5 - x^4 x^3 - px^2 qx 4$ is divisible by $(x 2)(x - 1),$ find the ordered pair $(p,q).$

Answer 1

Answer: The required ordered pair (p, q) is (-7, -12).

Step-by-step explanation: Given that (x+2)(x-1) divides the following polynomial f(x) :

`f(x)=x^5-x^4+x^3-px^2+qx+4.`

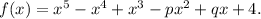
We are to find the ordered pair (p,q).

We have the following theorem :

Factor theorem : If (x-a) divides a polynomial h(x), then h(a) = 0.

According to the given information, we can say that (x+2) divides f(x). So, we get

`f(-2)=0\\\\\Rightarrow (-2)^5-(-2)^4+(-2)^3-p(-2)^2+q(-2)+4=0\\\\\Rightarrow -32-16-8-4p-2q+4=0\\\\\Rightarrow 2p+q=-26~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

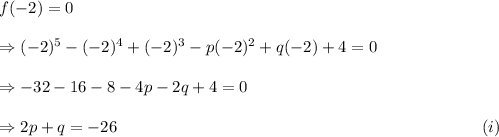
Also, (x-1) is a factor of f(x). So,

`f(1)=0\\\\\Rightarrow (1)^5-(1)^4+(1)^3-p(1)^2+q(1)+4=0\\\\\Rightarrow 1-1+1-p+q+4=0\\\\\Rightarrow p-q=5~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(ii)`

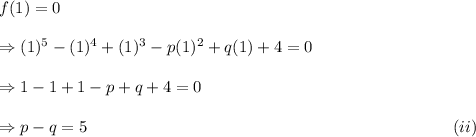
Adding equations (i) and (ii), we get

`3p=-21\\\\\Rightarrow p=-7.`

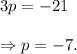
From equation (ii), we get

`-7-q=5\\\\\Rightarrow q=-12.`

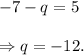
Thus, the required ordered pair (p, q) is (-7, -12).