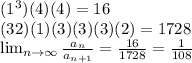Question

Define the double factorial of n, denoted n!!, as follows:n!!={1⋅3⋅5⋅⋅⋅⋅(n−2)⋅n} if n is odd{2⋅4⋅6⋅⋅⋅⋅(n−2)⋅n} if n is evenand (−1)!! =0!! =1.Find the radius of convergence for the given power series.[(8^n*n!*(3n+3)!*(2n)!!)/(2^n*[(n+9)!]^3*(4n+3)!!)]*(8x+6)^n

Answer 1

Radius of convergence of power series is
`\lim_(n \to \infty)(a_(n))/(a_(n+1))=(1)/(108)`

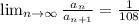
Explanation:

Given that:

n!! = 1⋅3⋅5⋅⋅⋅⋅(n−2)⋅n n is odd

n!! = 2⋅4⋅6⋅⋅⋅⋅(n−2)⋅n n is even

(-1)!! = 0!! = 1

We have to find the radius of convergence of power series:

`\sum_(n=1)^(\infty)[(8^(n)n!(3n+3)!(2n)!!)/(2^(n)[(n+9)!]^(3)(4n+3)!!)](8x+6)^(n)\\\\\sum_(n=1)^(\infty)[(8^(n)n!(3n+3)!(2n)!!)/(2^(n)[(n+9)!]^(3)(4n+3)!!)]2^(n)(4x+3)^(n)\\\\\sum_(n=1)^(\infty)[(8^(n)n!(3n+3)!(2n)!!)/([(n+9)!]^(3)(4n+3)!!)](x+(3)/(4))^(n)\\`

Power series centered at x = a is:

`\sum_(n=1)^(\infty)c_(n)(x-a)^(n)`

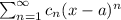
`\sum_(n=1)^(\infty)[(8^(n)n!(3n+3)!(2n)!!)/(2^(n)[(n+9)!]^(3)(4n+3)!!)](8x+6)^(n)\\\\\sum_(n=1)^(\infty)[(8^(n)n!(3n+3)!(2n)!!)/(2^(n)[(n+9)!]^(3)(4n+3)!!)]2^(n)(4x+3)^(n)\\\\\sum_(n=1)^(\infty)[(8^(n)4^(n)n!(3n+3)!(2n)!!)/([(n+9)!]^(3)(4n+3)!!)](x+(3)/(4))^(n)\\`

`a_(n)=[(8^(n)4^(n)n!(3n+3)!(2n)!!)/([(n+9)!]^(3)(4n+3)!!)]\\\\a_(n+1)=[(8^(n+1)4^(n+1)n!(3(n+1)+3)!(2(n+1))!!)/([(n+1+9)!]^(3)(4(n+1)+3)!!)]\\\\a_(n+1)=[(8^(n+1)4^(n+1)(n+1)!(3n+6)!(2n+2)!!)/([(n+10)!]^(3)(4n+7)!!)]`

Applying the ratio test:

`(a_(n))/(a_(n+1))=([(32^(n)n!(3n+3)!(2n)!!)/([(n+9)!]^(3)(4n+3)!!)])/([(32^(n+1)(n+1)!(3n+6)!(2n+2)!!)/([(n+10)!]^(3)(4n+7)!!)])`

`(a_(n))/(a_(n+1))=((n+10)^(3)(4n+7)(4n+5))/(32(n+1)(3n+4)(3n+5)(3n+6)+(2n+2))`

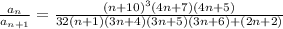
Applying n → ∞

`\lim_(n \to \infty)(a_(n))/(a_(n+1))= \lim_(n \to \infty)((n+10)^(3)(4n+7)(4n+5))/(32(n+1)(3n+4)(3n+5)(3n+6)+(2n+2))`

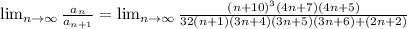
The numerator as well denominator of
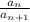`(a_(n))/(a_(n+1))` are polynomials of fifth degree with leading coefficients:

`(1^(3))(4)(4)=16\\(32)(1)(3)(3)(3)(2)=1728\\ \lim_(n \to \infty)(a_(n))/(a_(n+1))=(16)/(1728)=(1)/(108)`