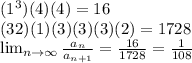Answer:
Radius of convergence of power series is
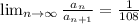
Explanation:
Given that:
n!! = 1⋅3⋅5⋅⋅⋅⋅(n−2)⋅n n is odd
n!! = 2⋅4⋅6⋅⋅⋅⋅(n−2)⋅n n is even
(-1)!! = 0!! = 1
We have to find the radius of convergence of power series:
![\sum_(n=1)^(\infty)[(8^(n)n!(3n+3)!(2n)!!)/(2^(n)[(n+9)!]^(3)(4n+3)!!)](8x+6)^(n)\\\\\sum_(n=1)^(\infty)[(8^(n)n!(3n+3)!(2n)!!)/(2^(n)[(n+9)!]^(3)(4n+3)!!)]2^(n)(4x+3)^(n)\\\\\sum_(n=1)^(\infty)[(8^(n)n!(3n+3)!(2n)!!)/([(n+9)!]^(3)(4n+3)!!)](x+(3)/(4))^(n)\\](https://img.qammunity.org/2021/formulas/mathematics/college/u3oyvei192ah569hz4pkoc30aknvko7s5s.png)
Power series centered at x = a is:
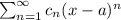
![\sum_(n=1)^(\infty)[(8^(n)n!(3n+3)!(2n)!!)/(2^(n)[(n+9)!]^(3)(4n+3)!!)](8x+6)^(n)\\\\\sum_(n=1)^(\infty)[(8^(n)n!(3n+3)!(2n)!!)/(2^(n)[(n+9)!]^(3)(4n+3)!!)]2^(n)(4x+3)^(n)\\\\\sum_(n=1)^(\infty)[(8^(n)4^(n)n!(3n+3)!(2n)!!)/([(n+9)!]^(3)(4n+3)!!)](x+(3)/(4))^(n)\\](https://img.qammunity.org/2021/formulas/mathematics/college/vyrf1730vll7g2muvijbuvmea204o8ba80.png)
![a_(n)=[(8^(n)4^(n)n!(3n+3)!(2n)!!)/([(n+9)!]^(3)(4n+3)!!)]\\\\a_(n+1)=[(8^(n+1)4^(n+1)n!(3(n+1)+3)!(2(n+1))!!)/([(n+1+9)!]^(3)(4(n+1)+3)!!)]\\\\a_(n+1)=[(8^(n+1)4^(n+1)(n+1)!(3n+6)!(2n+2)!!)/([(n+10)!]^(3)(4n+7)!!)]](https://img.qammunity.org/2021/formulas/mathematics/college/5nz855scma4obqbkj0frn9r9fsbfxfv96b.png)
Applying the ratio test:
![(a_(n))/(a_(n+1))=([(32^(n)n!(3n+3)!(2n)!!)/([(n+9)!]^(3)(4n+3)!!)])/([(32^(n+1)(n+1)!(3n+6)!(2n+2)!!)/([(n+10)!]^(3)(4n+7)!!)])](https://img.qammunity.org/2021/formulas/mathematics/college/wwwi1qbbbqy00eu2ev40cjsz4crmz1tcey.png)
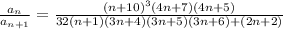
Applying n → ∞
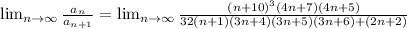
The numerator as well denominator of
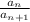 are polynomials of fifth degree with leading coefficients:
are polynomials of fifth degree with leading coefficients: