Question

An inscribed triangle with the hypotenuse being the diameter of the circle has angle A be 42 degrees. Angle C is 90 degrees. The area of the triangle ACK is 50cm^2. Find the radius of the circle

Answer 1

The Radius of circle is 7.15 cm

Explanation:

Given as :

A Triangle is inscribed into circle

The center of circle is O

The Diameter of circle = AK = d

The hypotenuse of triangle being the diameter of circle

The Area of triangle = 50 cm²

Let The radius of circle = r cm

The Triangle is right angle at c

So , ∠ACK = 90°

∠CAK = 42°

∠AKC = 180° - (90° + 42°)

So, ∠AKC = 48°

Now, ∵ Area of triangle ACK = 50 cm²

So,
`(1)/(2)` × AC × CK = 50

Or, AC × CK = 50 × 2

i.e , AC × CK = 100 ..........1

From figure

Sin 48° =
`(AC)/(AK)`

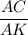
Or, 0.74 =
`(AC)/(d)`

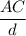
∴ AC = 0.74 d ..........2

Similarly

Sin 42° =
`(CK)/(AK)`

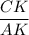
Or, 0.66 =
`(CK)/(d)`

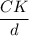
∴ CK = 0.66 d .............3

Putting eq 2 and 3 value into eq 1

i.e AC × CK = 100

Or, 0.74 d × 0.66 d = 100

Or, 0.4884 × d² = 100

∴ d² =
`(100)/(0.4884)`

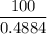
Or, d² = 204.75

Or, d =
`√(204.75)`

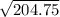
Or, d = 14.30

So, The diameter of circle = d = 14.30 cm

Now, Radius of circle =
`(\textrm diameter)/(2)`

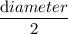
Or, r =
`(\textrm 14.30 cm)/(2)`

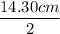
i.e r = 7.15 cm

So, The Radius of circle = r = 7.15 cm

Hence, The Radius of circle is 7.15 cm Answer