Answer:
The Radius of circle is 7.15 cm
Explanation:
Given as :
A Triangle is inscribed into circle
The center of circle is O
The Diameter of circle = AK = d
The hypotenuse of triangle being the diameter of circle
The Area of triangle = 50 cm²
Let The radius of circle = r cm
The Triangle is right angle at c
So , ∠ACK = 90°
∠CAK = 42°
∠AKC = 180° - (90° + 42°)
So, ∠AKC = 48°
Now, ∵ Area of triangle ACK = 50 cm²
So,
 × AC × CK = 50
× AC × CK = 50
Or, AC × CK = 50 × 2
i.e , AC × CK = 100 ..........1
From figure
Sin 48° =
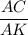
Or, 0.74 =
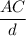
∴ AC = 0.74 d ..........2
Similarly
Sin 42° =
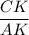
Or, 0.66 =
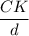
∴ CK = 0.66 d .............3
Putting eq 2 and 3 value into eq 1
i.e AC × CK = 100
Or, 0.74 d × 0.66 d = 100
Or, 0.4884 × d² = 100
∴ d² =
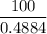
Or, d² = 204.75
Or, d =
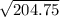
Or, d = 14.30
So, The diameter of circle = d = 14.30 cm
Now, Radius of circle =
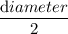
Or, r =
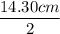
i.e r = 7.15 cm
So, The Radius of circle = r = 7.15 cm
Hence, The Radius of circle is 7.15 cm Answer