Answer: B. 264
Explanation:
Formula to calculate the sample size 'n' , if the prior estimate of the population proportion (p) is available:
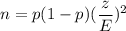
, where z = Critical z-value corresponds to the given confidence interval
E= margin of error
Let p be the population proportion of clear days.
As per given , we have
Prior sample size : n= 150
Number of clear days in that sample = 117
Prior estimate of the population proportion of clear days =
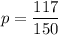
E= 0.05
The critical z-value corresponding to 95% confidence interval = z*= 1.95 (By z-table)
Then, the required sample size will be :
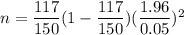
Simplify ,
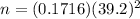
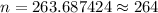
Hence, the sample size necessary to construct this interval =264
Thus the correct option is B. 264