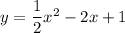Question

Type the correct answer in each box. Use numerals instead of words. If necessary, use / for the fraction bar.

Determine the equation for the parabola graphed below.
y =
x2 +
x +

Answer 1

`\large\boxed{y=(1)/(2)x^2-2x+1}`

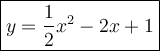
Explanation:

The vertex form of an equation of a parabola:

`y=a(x-h)^2+k`

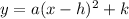
(h, k) - vertex

a - leading coefficient in equation y = ax² + bx + c

From the grap we can read coordinates of the vertex (2, -1) and y-intercept (0, 1).

Therefore h = 2, k = -1

Put the values of h, k and coordinates of the y-intercept to the equation of parabola:

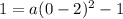`1=a(0-2)^2-1` add 1 to both sides

`1+1=a(2)^2-1+1`

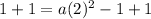
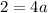`2=4a` divide both sides by 4

`(2)/(4)=(4a)/(4)\\\\(1)/(2)=a\to a=(1)/(2)`

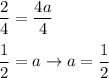
Therefore we have the equation:

`y=(1)/(2)(x-2)^2-1`

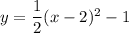
Convert to the standard form:

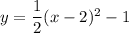`y=(1)/(2)(x-2)^2-1` use (a - b)² = a² - 2ab + b²

`y=(1)/(2)(x^2-2(x)(2)+2^2)-1`

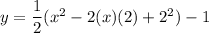
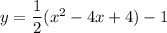`y=(1)/(2)(x^2-4x+4)-1` use the distributive property

`y=(1)/(2)x^2-(1)/(2)\cdot4x+(1)/(2)\cdot4-1`

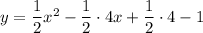
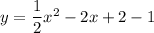`y=(1)/(2)x^2-2x+2-1` combine like terms

`y=(1)/(2)x^2-2x+1`