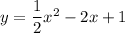Answer:
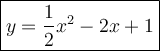
Explanation:
The vertex form of an equation of a parabola:

(h, k) - vertex
a - leading coefficient in equation y = ax² + bx + c
From the grap we can read coordinates of the vertex (2, -1) and y-intercept (0, 1).
Therefore h = 2, k = -1
Put the values of h, k and coordinates of the y-intercept to the equation of parabola:
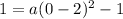 add 1 to both sides
add 1 to both sides
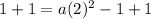
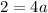 divide both sides by 4
divide both sides by 4
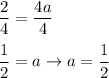
Therefore we have the equation:
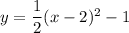
Convert to the standard form:
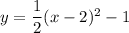 use (a - b)² = a² - 2ab + b²
use (a - b)² = a² - 2ab + b²

 use the distributive property
use the distributive property
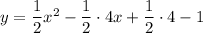
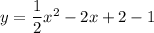 combine like terms
combine like terms