Answer:
$ 59.25
Explanation:
The given rates form an AP (Arithmetic Progression).
Let the cost of walking 1 dog be taken as the first term
and,
cost of walking 2 dogs as second term,
we notice that the price per dog is decreasing by 2.75 $ each time the number of dogs is increasing by 1.
So, it's safe to say that
In the AP:
First term is $ 40
Common difference is $ 2.75
Finding the charge to walk each of the eight dogs is like finding the 8th term of the given Series.
Formula for n-th term of a depreciating AP in terms of common difference(d) and first term(a):
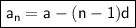
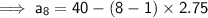
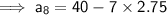
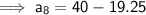
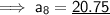
Answer:
Hence, the charge to walk each of the eight dogs is $ 20.75