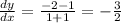Answer:
The slope of the tangent line is -3/2.
Explanation:
The slope of a tangent line is given by the derivative evaluated at the point of tangency.
To find the derivative dy/dx, use implicit differentiation.
The derivative of the first term is 2x.
The derivative of the second term is found by using the Product Rule.
The derivative of y is dy/dx.
The derivative of 3 is 0.
Differentiating each term produces
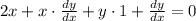
Solve for dy/dx.

Plug in the point (1, 1).