Answer:
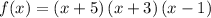 .
.
Explanation:
By the factor theorem, if a constant
 is zero of the polynomial
is zero of the polynomial
 ,
,
 would be a factor of this polynomial. (Notice how
would be a factor of this polynomial. (Notice how
 would indeed set the value of
would indeed set the value of
 to
to
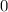 .)
.)
For instance, since
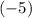 is a zero of the polynomial
is a zero of the polynomial
 ,
,
 would be a factor of
would be a factor of
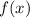 . Simplify this expression to get
. Simplify this expression to get
 .
.
Likewise, the zero
 would correspond to the factor
would correspond to the factor
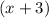 , while the zero
, while the zero
 would correspond to the factor
would correspond to the factor
 .
.
All three of these factors above are linear, and the degree of the variable
 in each factor is
in each factor is
 . Multiplying three such linear factors would give a polynomial of degree
. Multiplying three such linear factors would give a polynomial of degree
 .
.
Given the three factors, the expression of
 in factored form would be:
in factored form would be:
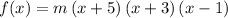 for some constant
for some constant
 .
.
When this expression is expanded, the constant
 would be the coefficient of the
would be the coefficient of the
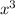 term (the leading term.) In other words,
term (the leading term.) In other words,
 is the leading coefficient of
is the leading coefficient of
 . This question has required this coefficient to be
. This question has required this coefficient to be
 . Thus,
. Thus,
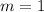 . The expression of
. The expression of
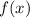 in factored form would be:
in factored form would be:
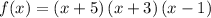 .
.