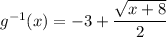Question

How do I find the inverse?

Answer 1

g(x) as given has no inverse because there are instances of two x values giving the same value of g(x). For instance,

x = -1 ⇒ g(-1) = 4 (-1 + 3)² - 8 = 8

x = -5 ⇒ g(-5) = 4 (-5 + 3)² - 8 = 8

Only a one-to-one function can have an inverse. g(x) is not one-to-one.

However, if we restrict the domain of g(x), we can find an inverse over that domain. Let
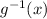`g^(-1)(x)` be the inverse of g(x). Then by definition of inverse function,

`g\left(g^(-1)(x)\right) = 4 \left(g^(-1)(x) + 3\right)^2 - 8 = x`

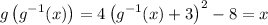
Solve for the inverse:

`4 \left(g^(-1)(x) + 3\right)^2 - 8 = x`

`4 \left(g^(-1)(x) + 3\right)^2 = x + 8`

`\left(g^(-1)(x) + 3\right)^2 = \frac{x + 8}4`

`\sqrt{\left(g^(-1)(x) + 3\right)^2} = \sqrt{\frac{x + 8}4}`

`\left| g^(-1)(x) + 3 \right| = \frac{√(x+8)}2`

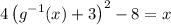
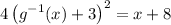
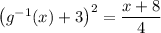
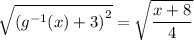
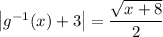
Recall the definition of absolute value:

`|x| = \begin{cases}x & \text{if }x\ge0\\-x&\text{if }x<0\end{cases}`

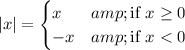
This means there are two possible solutions for the inverse of g(x) :

• if
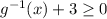`g^(-1)(x) + 3 \ge 0`, then

`g^(-1)(x) + 3 = \frac{√(x+8)}2 \implies g^(-1)(x) = -3+\frac{√(x+8)}2`

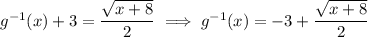
• otherwise, if
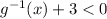`g^(-1)(x)+3<0`, then

`-\left(g^(-1)(x) + 3\right) = \frac{√(x+8)}2 \implies g^(-1)(x) = -3-\frac{√(x+8)}2`

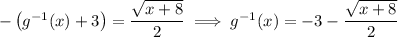
Which we choose as the inverse depends on how we restrict the domain of g(x). For example:

Remember that the inverse must satisfy

`g\left(g^(-1)(x)\right) = x`

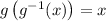
In the first case above,
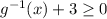`g^(-1)(x) + 3 \ge 0`, or
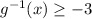`g^(-1)(x) \ge -3`. This suggests that we could restrict the domain of g(x) to be
`x \ge -3`.

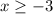Then as long as
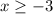`x \ge -3`, the inverse is

`g^(-1)(x) = -3+\frac{√(x+8)}2`