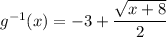g(x) as given has no inverse because there are instances of two x values giving the same value of g(x). For instance,
x = -1 ⇒ g(-1) = 4 (-1 + 3)² - 8 = 8
x = -5 ⇒ g(-5) = 4 (-5 + 3)² - 8 = 8
Only a one-to-one function can have an inverse. g(x) is not one-to-one.
However, if we restrict the domain of g(x), we can find an inverse over that domain. Let
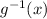 be the inverse of g(x). Then by definition of inverse function,
be the inverse of g(x). Then by definition of inverse function,
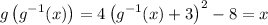
Solve for the inverse:
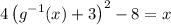
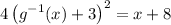
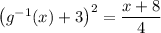
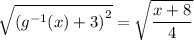
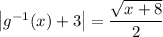
Recall the definition of absolute value:
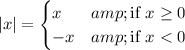
This means there are two possible solutions for the inverse of g(x) :
• if
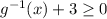 , then
, then
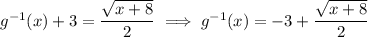
• otherwise, if
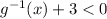 , then
, then
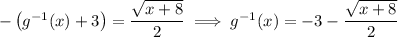
Which we choose as the inverse depends on how we restrict the domain of g(x). For example:
Remember that the inverse must satisfy
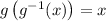
In the first case above,
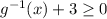 , or
, or
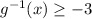 . This suggests that we could restrict the domain of g(x) to be
. This suggests that we could restrict the domain of g(x) to be
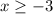 .
.
Then as long as
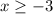 , the inverse is
, the inverse is