Answer:
See below for answers and explanations
Explanation:
Problem 1
Rewrite and add each vector:

Find the magnitude of the resulting vector:
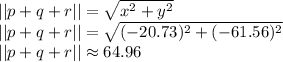
Therefore, the best answer is D) 64.959
Problem 2
Think of the vectors like this:
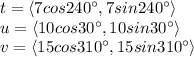
By adding the vectors, we have:

Since the direction of a vector is
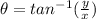 , we have:
, we have:
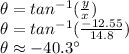
Don't forget to take into account that the resulting vector is in Quadrant IV since the horizontal component is positive and the vertical component is negative, so we will add 360° to our angle to get the result:
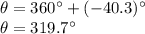
Therefore, the best answer is D) 320°
Problem 3
Again, rewrite the vectors and add them:
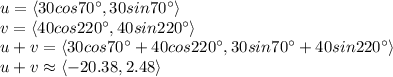
Using the direction formula:
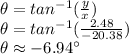
As the vector is located in Quadrant II, we need to add 180° to our angle:
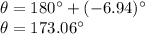
Therefore, the best answer is D) 173°
Problem 4
Using scalar multiplication:
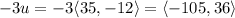
Find the magnitude of the resulting vector:
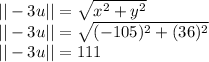
Find the direction of the resulting vector:
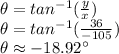
As the vector is located in Quadrant II, we need to add 180° to our angle:
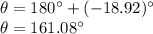
Therefore, the best answer is C) 111; 161°
Problem 5
Using scalar multiplication:
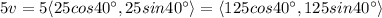
Since the direction of the angle doesn't change in scalar multiplication, it only affects the magnitude, so the magnitude of the resulting vector would be
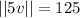 , making the correct answer C) 125; 200°
, making the correct answer C) 125; 200°