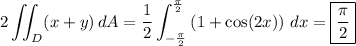Given that y = cos(x) makes up part of the boundary of C, I suspect you mean the given points to be (-π/2, 0) and (π/2, 0).
I also assume the given vector field is
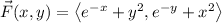
Since
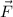 has no singularities on C or in its interior, Green's theorem applies:
has no singularities on C or in its interior, Green's theorem applies:
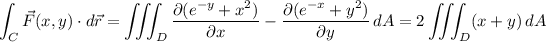
where D is the interior of C, the region
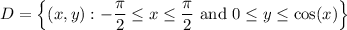
The integral then reduces to
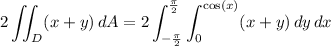
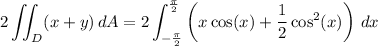
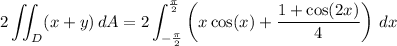
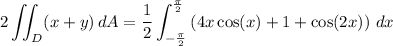
Since 4x cos(x) is an odd function over the symmetric interval [-π/2, π/2], its contribution to the integral is 0, and the remaining integral is trivial.