Question

Can someone help please

Answer 1

Answer: 15x^(7/3) - 8x^(7/4) + x + 9000

=========================================================

Step-by-step explanation:

If you know the cost function C(x), to find the marginal cost, we apply the derivative.

Marginal cost = derivative of cost function

Marginal cost = C ' (x)

Since we're given the marginal cost, we'll apply the antiderivative (aka integral) to figure out what C(x) is. This reverses the process described above.

`\text{Cost} = \text{antiderivative of marginal cost}\\\\\displaystyle C(x) = \int \left(35x^(4/3) - 14x^(3/4) + 1\right)dx\\\\`

`C(x) = (1)/(1+4/3)*35x^(4/3+1) - (1)/(1+3/4)*14x^(3/4+1) + x + D\\\\C(x) = (1)/(7/3)*35x^(7/3) - (1)/(7/4)*14x^(7/4) + x + D\\\\C(x) = (3)/(7)*35x^(7/3) - (4)/(7)*14x^(7/4) + x + D\\\\C(x) = 15x^(7/3) - 8x^(7/4) + x + D\\\\`

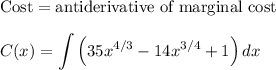
D represents a fixed constant. I would have used C as the constant of integration, but it's already taken by the cost function C(x).

To determine the value of D, we plug in x = 0 and C(x) = 9000. This is because we're told the fixed costs are $9000. This means that when x = 0 units are made, you still have $9000 in costs to pay. This is the initial value. You'll find that all of this leads to D = 9000 because everything else zeros out.

Therefore, we go from this

`C(x) = 15x^(7/3) - 8x^(7/4) + x + D\\\\`

to this

`C(x) = 15x^(7/3) - 8x^(7/4) + x + 9000\\\\`

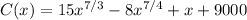
which is the final answer.