Answer:
Approximately
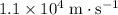 if air friction is negligible.
if air friction is negligible.
Step-by-step explanation:
Let
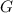 denote the gravitational cosntant. Let
denote the gravitational cosntant. Let
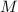 denote the mass of the earth. Lookup the value of both values:
denote the mass of the earth. Lookup the value of both values:
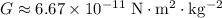 while
while
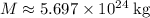 .
.
Let
 denote the mass of the meteor.
denote the mass of the meteor.
Let
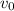 denote the initial velocity of the meteor. Let
denote the initial velocity of the meteor. Let
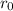 denote the initial distance between the meteor and the center of the earth.
denote the initial distance between the meteor and the center of the earth.
Let
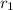 denote the distance between the meteor and the center of the earth just before the meteor lands.
denote the distance between the meteor and the center of the earth just before the meteor lands.
Let
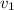 denote the velocity of the meteor just before landing.
denote the velocity of the meteor just before landing.
The radius of planet earth is approximately
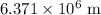 . Therefore:
. Therefore:
- At an altitude of
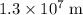 about the surface of the earth, the meteor would be approximately
about the surface of the earth, the meteor would be approximately
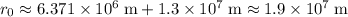 away from the surface of planet earth.
away from the surface of planet earth. - The meteor would be only
 away from the center of planet earth just before landing.
away from the center of planet earth just before landing.
Note the significant difference between the two distances. Thus, the gravitational field strength (and hence acceleration of the meteor) would likely have changed significant during the descent. Thus, SUVAT equations would not be appropriate.
During the descent, gravitational potential energy (
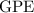 ) of the meteor was turned into the kinetic energy (
) of the meteor was turned into the kinetic energy (
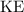 ) of the meteor. Make use of conservation of energy to find the velocity of the meteor just before landing.
) of the meteor. Make use of conservation of energy to find the velocity of the meteor just before landing.
Initial
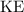 of the meteor:
of the meteor:
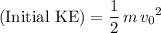 .
.
Initial
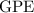 of the meteor:
of the meteor:
 .
.
(Note the negative sign in front of the fraction.)
Just before landing, the
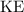 and the
and the
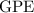 of this meteor would be:
of this meteor would be:
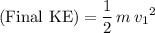 .
.
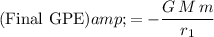 .
.
If the air friction on this meteor is negligible, then by the conservation of mechanical energy:
 .
.
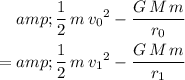 .
.
Rearrange and solve for
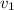 , the velocity of the meteor just before landing:
, the velocity of the meteor just before landing:
 .
.
Substitute in the values and evaluate:
![\begin{aligned}v_(1) &= \sqrt{{v_(0)}^(2) - G\, M\, \left((1)/(r_(1)) - (1)/(r_(0))\right)} \\ &\approx \sqrt{\begin{aligned}(& 6.5 * 10^(3)\; {\rm m \cdot s^(-1)}) \\ & - [6.67 * 10^(-11)\; {\rm N \cdot {m}^(2)\cdot {kg}^(2) * 5.697\; {\rm kg}}\\ &\quad\quad * (1 / (6.371 * 10^(6)\; {\rm m}) - 1 / (1.9371 * 10^(7)\; {\rm m}))]\end{aligned}} \\ &\approx 1.1 * 10^(4)\; {\rm m\cdot {s}^(-1)}\end{aligned}](https://img.qammunity.org/2023/formulas/physics/college/n6nlfo2ub58fhcukgu4cxei56nhqaj0mtt.png) .
.
(Note that assuming a constant acceleration of
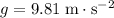 would give
would give
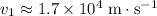 , an inaccurate approximation.
, an inaccurate approximation.