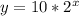The form
 has two unknowns, namely
has two unknowns, namely
 and
and
 , so you would need to have two points to find the equation (which you do). Once you have your two points, you can create a system of equations by plugging in the x and y coordinates like below:
, so you would need to have two points to find the equation (which you do). Once you have your two points, you can create a system of equations by plugging in the x and y coordinates like below:

One thing you may remember is that ANY number to the power of 0 equals 1. Knowing that, we can replace
 in the first equation with 1. Since 1 multiplied by any number is just that same number, that leaves
in the first equation with 1. Since 1 multiplied by any number is just that same number, that leaves
 alone in the first equation.
alone in the first equation.
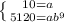
The first equation now tells us that
 is 10, so we can plug 10 in for
is 10, so we can plug 10 in for
 in the other equation.
in the other equation.
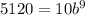
Now we can divide both sides by 10 to isolate
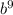 .
.
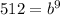
To get
 alone, we have to take the 9th root of both sides.
alone, we have to take the 9th root of both sides.
![\sqrt[9]{512} =\sqrt[9]{b^9}](https://img.qammunity.org/2023/formulas/mathematics/college/utlwme7llwius75s0r3pywzjvhkkohrjtr.png)
That gives us:
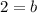
We can now plug
 and
and
 into the form they gave us to get:
into the form they gave us to get: