Question

What is the derivative of 1/square root 4x.

Answer 1

`\displaystyle (d)/(dx) \bigg[ (1)/(√(4x)) \bigg] = \frac{-1}{4x^\bigg{(3)/(2)}}`

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

Exponential Properties

• Exponential Property [Rewrite]:
  `\displaystyle b^(-m) = (1)/(b^m)`
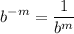
• Exponential Property [Root Rewrite]:
  `\displaystyle \sqrt[n]{x} = x^{(1)/(n)}`

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Derivative Rule [Basic Power Rule]:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Explanation:

Step 1: Define

Identify.

`\displaystyle (d)/(dx) \bigg[ (1)/(√(4x)) \bigg]`

Step 2: Differentiate

1. Simplify:
   `\displaystyle (d)/(dx) \bigg[ (1)/(√(4x)) \bigg] = \bigg( (1)/(2√(x)) \bigg)'`
2. Rewrite [Derivative Property - Multiplied Constant]:
   `\displaystyle (d)/(dx) \bigg[ (1)/(√(4x)) \bigg] = (1)/(2) \bigg( (1)/(√(x)) \bigg)'`
3. Rewrite [Exponential Rule - Root Rewrite]:
   `\displaystyle (d)/(dx) \bigg[ (1)/(√(4x)) \bigg] = (1)/(2) \bigg( \frac{1}{x^\Big{(1)/(2)}} \bigg)'`
4. Rewrite [Exponential Rule - Rewrite]:
   `\displaystyle (d)/(dx) \bigg[ (1)/(√(4x)) \bigg] = (1)/(2) \bigg( x^\bigg{(-1)/(2)} \bigg)'`
5. Derivative Rule [Basic Power Rule]:
   `\displaystyle (d)/(dx) \bigg[ (1)/(√(4x)) \bigg] = (1)/(2) \bigg( (-1)/(2) x^\bigg{(-3)/(2)} \bigg)`
6. Simplify:
   `\displaystyle (d)/(dx) \bigg[ (1)/(√(4x)) \bigg] = (-1)/(4) x^\bigg{(-3)/(2)}`
7. Rewrite [Exponential Rule - Rewrite]:
   `\displaystyle (d)/(dx) \bigg[ (1)/(√(4x)) \bigg] = \frac{-1}{4x^\bigg{(3)/(2)}}`

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Differentiation