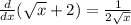Explanation:
If the equation is
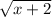
Then, here is the answer.
The definition of a derivative is
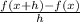
Also note that we want h to be a small, negligible value so we let h be a value that is infinitesimal small.
So we get
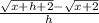
Multiply both equations by the conjugate.
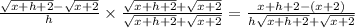
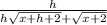
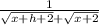
Since h is very small, get rid of h.
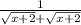
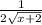
So the derivative of
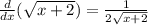
Part 2: If your function is
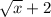
Then we get
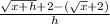
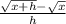
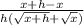
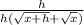
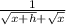
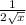
So