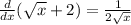Question

Use the definition of the derivative as a limit to find the
derivative f′ where f(x)= √ x+2.

Answer 1

Explanation:

If the equation is

`√(x + 2)`

Then, here is the answer.

The definition of a derivative is

`(f(x + h) - f(x))/(h)`

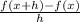
Also note that we want h to be a small, negligible value so we let h be a value that is infinitesimal small.

So we get

`( √(x + h + 2) - √(x + 2) )/(h)`

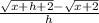
Multiply both equations by the conjugate.

`( √(x + h + 2) - √(x + 2) )/(h) * ( √(x + h + 2) + √(x + 2) )/( √(x + h + 2) + √(x + 2) ) = (x + h + 2 - (x + 2))/(h √(x + h + 2) + √(x + 2) )`

`(h)/(h √(x + h + 2) + √(x + 2) )`

`(1)/( √(x + h + 2) + √(x + 2) )`

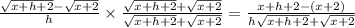
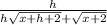
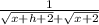
Since h is very small, get rid of h.

`(1)/( √(x + 2) + √(x + 2) )`

`(1)/(2 √(x + 2) )`

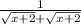
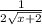
So the derivative of

`(d)/(dx) ( √(x + 2) ) = (1)/(2 √(x + 2) )`

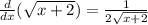
Part 2: If your function is

`√(x) + 2`

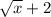
Then we get

`( √(x + h) + 2 - ( √(x) + 2) )/(h)`

`( √(x + h) - √(x) )/(h)`

`(x + h - x)/(h( √(x + h) + √(x)) )`

`(h)/(h( √(x + h) + √(x) ) )`

`(1)/( √(x + h) + √(x) )`

`(1)/(2 √(x) )`

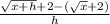
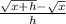
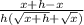
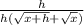
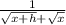
So

`(d)/(dx) ( √(x) + 2) = (1)/(2 √(x) )`