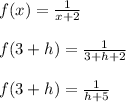If x is the only thing in the denominator, then,
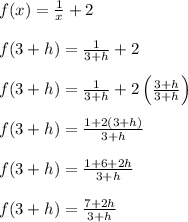
We replace every copy of x with 3+h, as shown in the second step. Afterwards, we can optionally simplify to form one big fraction.
---------------------------------------------------------------------------
Or if the "x+2" is in the denominator, then we have these steps: