Answer:
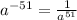
Explanation:
When you're multiplying two powers with the same base (in our case, a) you add together the exponents.
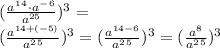
Now, when you are dividing two powers with the same base (in our case, a again) you subtract the exponents:
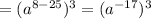
Finally, when you're calculating the power of a power, you multiply the exponents together:
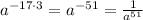
At this point you just have to choose - or check with your book/teacher if you prefer a negative exponent, or a fraction.