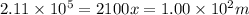Question

A car travelling at 79.3 Km/h on a highway has 4.22x10 5 J of kinetic energy.

a. What is the mass of the car?

b. If brakes are applied with a force of 2100 N, what distance will it take for the car to slow down to a speed of 56 Km/h?

Answer 1

`1.74*10^3 kg; 100m`

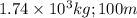
Step-by-step explanation:

Step a: mass of the car. Let's grab the definition of kinetic energy:
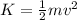`K= \frac12 mv^2`. We have K, we have v (which we should convert in meters per second, dividing by 3.6) to get:
`4.22*10^5 = \frac12m(22.03)^2 \rightarrow m= 2*4.22 / 495.22 * 10^5 = 1.74 * 10^3 kg`

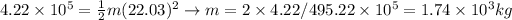
Point a is done.

Now for the (b)reaking part. (I'm sorry, it's an horrible joke, but I couldn't resist)

In theory we have the mass, we have the force, so we could find the acceleration, find how long it takes to slow down, and then find the distance traveled. Too long. Let's do things more easily: when the car slows down to 56 km/h it will have a different kinetic energy. The difference in kinetic energy is the work done by the breaking force ofer the slowing distance.

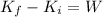`K_f-K_i=W` A quick note on signs: if you look carefully the final kinetic energy will be less than the initial value, thus the work will be negative: it means it's correct, since the work is against the motion, slowing it down. Let's get calculating, first by converting 56 kmh in m/s (15,56 m/s), then finding the final kinetic energy:

`K_f =\frac12 (1.74*10^3) (15.56)^2 =2.11 * 10^5 J`

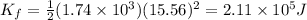
The difference will be the work done by the force, or

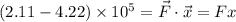`(2.11 - 4.22) * 10^5 = \vec F\cdot \vec x=Fx` where we are assuming that force and displacement have the same line of actions to simplify the dot product.

`2.11* 10^5 = 2100x = 1.00* 10^2 m`