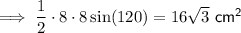Answer:
∠ABC = 120°
ΔABC = 16√3 cm²
Explanation:
Part (a)
Sum of interior angles of a regular polygon = (n - 2) × 180°
(where n is the number of sides)
⇒ Sum of interior angles of a regular hexagon = (6 - 2) × 180° = 720°
All the interior angles in a regular polygon are equal.
⇒ Interior angle = sum of interior angles ÷ number of sides
⇒ ∠ABC = 720° ÷ 6
⇒ ∠ABC = 120°
------------------------------------------------------------------------
Part (b)
Use the sine rule for area of a triangle:
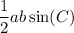
(where a and b are the sides and C is the included angle)
Given:
- a = 8
- b = 8
- C = ∠ABC = 120°
Substituting values into the formula: