Hi there!
The equation for the gravitational potential energy of a mass in orbit is:
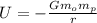
Where:
m₀ = mass of object (kg)
mp = mass of planet (kg)
r = radius (from CENTER of the planet)
G = Gravitational constant
The change of gravitational potential energy is given as:
ΔU = Uf - Ui
Thus, we can calculate each:
Uf:
r = radius of earth + radius of orbit
6,378,000 m + 25,000 m = 6,403,000 m
We can plug in the given values into the equation:
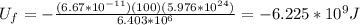
Ui:
r = radius of earth
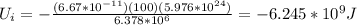
Subtract:
-6.225 × 10⁹ - (-6.245 × 10⁹) = 2.46 × 10⁷ J