Question

A 100 kg satellite is launched into a 25 km orbit. What is the change in its gravitational potential energy? The mass of the earth is 5.976 × 1024 kg and the radius of the earth is 6.378 × 106 m.

Answer 1

Hi there!

The equation for the gravitational potential energy of a mass in orbit is:

`U = -(Gm_om_p)/(r)`

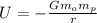
Where:

m₀ = mass of object (kg)

mp = mass of planet (kg)

r = radius (from CENTER of the planet)

G = Gravitational constant

The change of gravitational potential energy is given as:

ΔU = Uf - Ui

Thus, we can calculate each:

Uf:

r = radius of earth + radius of orbit

6,378,000 m + 25,000 m = 6,403,000 m

We can plug in the given values into the equation:

`U_f= -((6.67*10^(-11))(100)(5.976*10^(24)))/(6.403*10^(6)) = -6.225*10^9 J`

Ui:

r = radius of earth

`U_i= -((6.67*10^(-11))(100)(5.976*10^(24)))/(6.378*10^(6)) = -6.245*10^9 J`

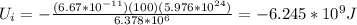
Subtract:

-6.225 × 10⁹ - (-6.245 × 10⁹) = 2.46 × 10⁷ J