Answer:
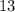 and
and
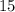 .
.
Explanation:
The difference between two consecutive odd integers is
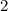 .
.
Let
 denote the smaller one of the two numbers (
denote the smaller one of the two numbers (
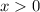 .) The other number would be
.) The other number would be
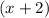 .
.
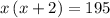 .
.
Thus,
 .
.
Solve this equation for
 using the quadratic formula:
using the quadratic formula:
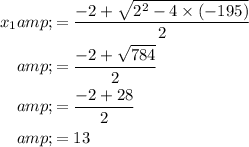 .
.
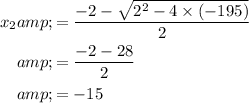 .
.
Only
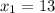 is a valid solution since
is a valid solution since
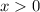 by assumption.
by assumption.
Therefore, the smaller one of the two odd numbers would be
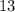 . The other integer would be
. The other integer would be
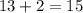 .
.