Question

there are 28 tables for customers at mesa grill resturant. the tablesnare either two-seat tables or four-seat tables. when all tables are full, there will be 90 customers in the restaurant. how many two-seat tables are at the restaurant

Answer 1

Answer: 11

Explanation:

This is a problem of solving word problems using systems of equations.

Let's denote 2-seat tables by x and 4-seat tables by y. Therefore, their sum will be the total number of tables, which is 28. So, x + y = 28.

Now, let's concentrate on the number of customers. It says that 'when all tables are full, there will be 90 customers in the restaurant'. Therefore if we seat 2 people on each 2-seat table(x), their total number will be 2x and if we seat 4 people on each 4-seat number(y), their total number will be 4y. Hence, 2x + 3y = 90.

Now, we have a system with two equations:

`\left \{ {{x + y = 28} \atop {2x + 4y = 90}} \right.`

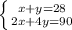
Multiply the first line by -4.

`\left \{ {{-4x -4y = -112} \atop {2x + 4y = 90}} \right.`

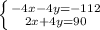
Now, by adding up these two equations, we get the following:

-2x = -22

x = 11

This means that the restaurant has 11 two-seat tables.

Answer 2

Explanation :-

Let's assume –

• Number of two-seat tables be "x"

`\qquad` According to the question :-

`\qquad \pmb{\sf\longrightarrow 4 * (28−x)+2 * x=90}`

`\qquad \pmb{\sf\longrightarrow 112−4x+2x=90}`

`\qquad \pmb{\sf\longrightarrow 112−2x=90}`

`\qquad \pmb{\sf\longrightarrow −2x=90−112}`

`\qquad \pmb{\sf\longrightarrow −2x=−22}`

`\qquad \pmb{\sf\longrightarrow 2 x=22}`

`\qquad \pmb{\sf\longrightarrow x= \cancel{(22)/(2)}}`

`\qquad \longrightarrow {\pink{\underline{\underline{\pmb{\sf{ x= 11}}}}}}`

Therefore –

• Number of two-seat tables are 11.

▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬