Answer: 11
Explanation:
This is a problem of solving word problems using systems of equations.
Let's denote 2-seat tables by x and 4-seat tables by y. Therefore, their sum will be the total number of tables, which is 28. So, x + y = 28.
Now, let's concentrate on the number of customers. It says that 'when all tables are full, there will be 90 customers in the restaurant'. Therefore if we seat 2 people on each 2-seat table(x), their total number will be 2x and if we seat 4 people on each 4-seat number(y), their total number will be 4y. Hence, 2x + 3y = 90.
Now, we have a system with two equations:
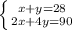
Multiply the first line by -4.
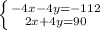
Now, by adding up these two equations, we get the following:
-2x = -22
x = 11
This means that the restaurant has 11 two-seat tables.