Question

Can someone help me with this? i don’t quite understand this.

Answer 1

Step 1) Rotate 90 degrees counterclockwise around the origin

Step 2) Shift 5 units down

=======================================================

Step-by-step explanation:

Focus on one of the corner points of figure S.

I'll focus on (9,1)

Apply a 90 degree counterclockwise rotation on this point, and rotate it around the origin.

The rotation rule is
`(x,y) \to (-y,x)`

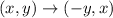
This means
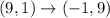`(9,1) \to (-1,9)` meaning (9,1) rotates to (-1,9)

Notice that (9,1) on figure S corresponds to (-1,4) on figure T.

This means after arriving to (-1,9), we need to somehow apply a shifting translation to get to (-1,4)

To get from (-1,9) to (-1,4) we shift the point down 5 units.

-----------------------

To recap:

• We rotated (9,1) around the origin 90 degrees counterclockwise to get to (-1,9)
• Then we shifted (-1,9) down 5 units to get to (-1,4)

If you apply that rotation and shifting rule to each of the four corner points of figure S, then you'll end up with figure T.

Figure S is known as the preimage while figure T is the image.