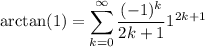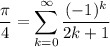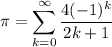Question

find a series expansion for pi using the Maclaurin expansion for arctan(x) and the fact that tan(pi/4)

Answer 1

Recall that for |x| < 1, we have

`\displaystyle \frac1{1-x} = \sum_(k=0)^\infty x^k`

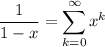
It follows that, for |-x²| = |x|² < 1, or just |x| < 1,

`\displaystyle \frac1{1+x^2} = \frac1{1-(-x^2)} = \sum_(k=0)^\infty (-x^2)^k = \sum_(k=0)^\infty (-1)^k x^(2k)`

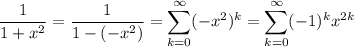
Taking the antiderivative of both sides gives us

`\displaystyle \arctan(x) = C + \sum_(k=0)^\infty ((-1)^k)/(2k+1) x^(2k+1)`

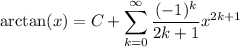
where C is a constant, which we determine to be 0, since taking x = 0 on both sides makes the series vanish, while arctan(0) = 0 since 0 = tan(0). So

`\displaystyle \arctan(x) = \sum_(k=0)^\infty ((-1)^k)/(2k+1) x^(2k+1)`

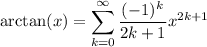
Since tan(π/4) = 1, it follows that π/4 = arctan(1), so in the series we replace x = 1, then solve for π :

`\displaystyle \arctan(1) = \sum_(k=0)^\infty ((-1)^k)/(2k+1) 1^(2k+1)`

`\displaystyle \frac\pi4 = \sum_(k=0)^\infty ((-1)^k)/(2k+1)`

`\displaystyle \pi = \sum_(k=0)^\infty (4(-1)^k)/(2k+1)`

`\pi = 4 - \frac43 + \frac45 - \frac47 +\cdots`