Answer:
The length of missing side of triangle is 13 cm.
Explanation:
Solution :
Here, we have given that the two sides of triangle are 5 cm and 12 cm.
Finding the third side of triangle by pythagoras theorem formula :
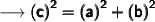
Substituting all the given values in the formula to find the third side of triangle :
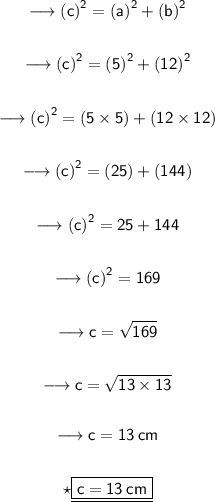
Hence, the length of missing side is 13 cm.
