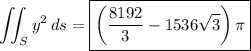Question

Evaluate the surface integral. S y2 ds s is the part of the sphere x2 + y2 + z2 = 64 that lies inside the cylinder x2 + y2 = 16 and above the xy-plane.

Answer 1

An alternative solution to the one I linked in the comments:

Let

z = f(x, y) = √(64 - x² - y²)

Then the integral of y² over the surface S is

`\displaystyle \iint_S y^2 \, ds = \iint\limits_(x^2+y^2\le16) y^2 \sqrt{1 + \left((\partial f)/(\partial x)\right)^2 + \left((\partial f)/(\partial y)\right)^2} \, dx \, dy`

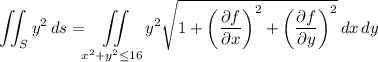
We have

∂f/∂x = -x/√(64 - x² - y²)

∂f/∂y = -y/√(64 - x² - y²)

so that the integrand simplifies to

`\displaystyle \iint_S y^2 \, ds = \iint\limits_(x^2+y^2\le16) y^2 \sqrt{1 + (x^2)/(64-x^2-y^2) + (y^2)/(64-x^2-y^2)} \, dx \, dy`

`\displaystyle \iint_S y^2 \, ds = \iint\limits_(x^2+y^2\le16) y^2 \sqrt{(64)/(64-x^2-y^2)} \, dx \, dy`

`\displaystyle \iint_S y^2 \, ds = 8 \iint\limits_(x^2+y^2\le16) (y^2)/(√(64-x^2-y^2)) \, dx \, dy`

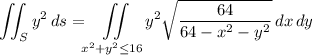
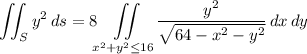
To compute the remaining integral, convert to polar coordinates using

x = r cos(θ)

y = r sin(θ)

dx dy = r dr dθ

The region x² + y² ≤ 16 is given by the set

D = {(r, θ) : 0 ≤ r ≤ 4 and 0 ≤ θ ≤ 2π}

Then the integral becomes

`\displaystyle \iint_S y^2 \, ds = 8 \int_0^(2\pi) \int_0^4 ((r\sin(\theta))^2)/(√(64-r^2)) (r \, dr \, d\theta)`

`\displaystyle \iint_S y^2 \, ds = 8 \int_0^(2\pi) \int_0^4 (r^3 \sin^2(\theta))/(√(64-r^2)) \, dr \, d\theta`

`\displaystyle \iint_S y^2 \, ds = 8 \left(\int_0^(2\pi) \sin^2(\theta) \, d\theta\right) \left(\int_0^4 (r^3)/(√(64-r^2)) \, dr\right)`

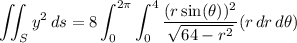
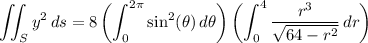
Now,

`\displaystyle \int_0^(2\pi) \sin^2(\theta) \, d\theta = \frac12 \int_0^(2\pi) (1-\cos(2\theta)) \, d\theta = \pi`

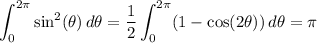
and by substituting u = 64 - r²,

`\displaystyle \int_0^4 (r^3)/(√(64-r^2)) \, dr = -\frac12 \int_(64)^(48) (64-u)/(\sqrt u) \, du`

`\displaystyle \int_0^4 (r^3)/(√(64-r^2)) \, dr = \frac12 \int_(48)^(64) \left(64u^(-\frac12) - u^(\frac12)\right) \, du`

`\displaystyle \int_0^4 (r^3)/(√(64-r^2)) \, dr = \frac{1024}3 - 192√(3)`

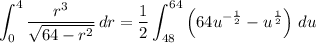
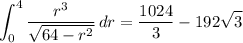
So, the surface integral has a value of

`\displaystyle \iint_S y^2 \, ds = \boxed{\left(\frac{8192}3 - 1536 \sqrt3\right) \pi}`