Answer: The constant rate change would be
 .
.
Step-by-step explanation: The general rate of change can be found by using the difference quotient formula. To find the average rate of change over an interval, enter a function with an interval: f (x) =
 , [2,3]
, [2,3]
Write y =
 x - 20 as a function which is f (x) =
x - 20 as a function which is f (x) =
 x - 20
x - 20
Consider the difference quotient formula which is
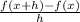 .
.
Find the components of the definition.
 simplify then it would be
simplify then it would be
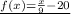 .
.
Lastly plug in all the components.
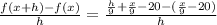
After solving all this the answer would be
