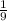Question

What is the constant rate of change for this equation y = 1/9x-20 ?​

Answer 1

Answer: The constant rate change would be
`(1)/(9)`.

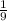Step-by-step explanation: The general rate of change can be found by using the difference quotient formula. To find the average rate of change over an interval, enter a function with an interval: f (x) =
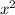`x^(2)` , [2,3]

Write y =
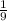`(1)/(9)`x - 20 as a function which is f (x) =
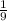`(1)/(9)`x - 20

Consider the difference quotient formula which is
`(f (x +h) - f (x) )/(h)`.

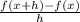Find the components of the definition.
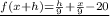`\frac{f (x+h) = (h)/(9) + (x)/(9) - 20}`simplify then it would be
`\frac{f (x) = (x)/(9) - 20 }`.

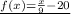Lastly plug in all the components.

`(f (x + h) - f (x))/(h) = ((h)/(9) +(x)/(9) - 20 - ((x)/(9) - 20) )/(h)`

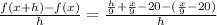
After solving all this the answer would be
`(1)/(9)`

Answer 2

like:-

1/9x20 = 2 2/9

1/9-20 = 19 8/9

Explanation:

I'm not sure