The lines represented by the equations
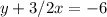 and
and
 are neither parallel nor perpendicular.
are neither parallel nor perpendicular.
To determine the relationship between the lines represented by the equations
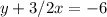 and
and
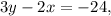
The slope-intercept form
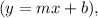 where m is the slope and b is the y-intercept.
where m is the slope and b is the y-intercept.
For
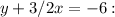
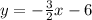
The slope (m) is -3/2.
For
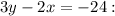
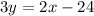
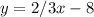
The slope (m) is 2/3.
Since the slopes are different (-3/2 and 2/3), the lines are not parallel.
To determine if they are perpendicular, we can check if the product of their slopes is -1.
However, in this case, the product is not -1 (-3/2 * 2/3 = -1).
Therefore, the lines are neither parallel nor perpendicular.