Answer:
12.5 m/s
Step-by-step explanation:
By conservation of momentum, we have that:
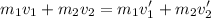
Because the two objects combine after collision, they will have the same velocity:
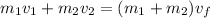
Substitute and solve for final velocity:

In conclusion, the final velocity of the system will be 12.5 m/s.