Answer:
9) y = -200x + 1200
11) slope = -2
15) $2,450
16) 9 days
Explanation:
9) Given the two points from the graph:
Let (x₁, y₁) = (0, 1200)
(x₂, y₂) = (1, 1000)
Substitute these values into the following slope formula:
m = (y₂ - y₁)/(x₂ - x₁)
m = (1000 - 1200)/(1 - 0)
m = -200/1
m = -200
The slope of the line is -200.
Next, we need to determine the y-intercept, which is the point on the graph where it crosses the y-axis. Upon observing the graph, it shows that the line crosses at point (0, 1200). The y-coordinate of this ordered pair is the value of the y-intercept, b = 1200.
Therefore, the linear equation in slope-intercept form is y = -200x + 1200.
11) Given the points, (5, -18) and (-4, 0):
Let (x₁, y₁) =(5, -18)
(x₂, y₂) = (-4, 0)
Substitute these values into the following slope formula:
m = (y₂ - y₁)/(x₂ - x₁)
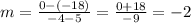
Therefore, the slope of the line is -2.
15) Solve:
Given the fixed fee of $200, and the $150 per hour after the initial meeting:
We can represent these in slope-intercept form:
y = 150x + 200
y = total cost for the Attorney's services
x = number of hours worked.
The y-intercept in this given problem is $200, which represents the flat fee charged for the initial meeting. While the slope in this equation is $150, which is the hourly rate that an Attorney charges his clients after the initial meeting.
If an Attorney works for 15 hours, then:
Let x = 15, and substitute its value into the equation to find the total cost:
y = 150x + 200
y = 150(15) + 200
y = 2,250 + 200
y = 2,450
Therefore, a client will pay a total of $2,450 for an Attorney's 15 hours of work.
16) Solve:
Given the water level on a Lake of 165 inches after a rainstorm, and the water level's receding rate of 3 inches per day:
We can establish the following linear equation to model this given problem:
L = -3d + 165
Where:
L = represents the water level of the Lake
d = number of days that the water level recedes
In order to find the number of days it will take before the water level recedes to 84 inches:
Substitute the value of L = 84 into the equation:
L = -3d + 165
84 = -3d + 165
Subtract 165 from both sides:
84 - 165 = 3d + 165 - 165
-27 = -3d
Divide both sides by -3:
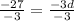
9 = d
Therefore, it will take 9 days for the water level to be at 84 inches.