Answer:
 or
or
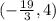
Explanation:
Given the systems of linear equations, 3x + 6y = 5 and -3x - 3y = 7:
Equation 1: 3x + 6y = 5
Equation 2: -3x - 3y = 7
The best method to use for the given system is the process of elimination, since the coefficients of x in both equations have opposite signs.
Step 1: Add both equations:
3x + 6y = 5
-3x - 3y = 7
3y = 12
Step 2: Divide both sides by 3:
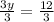
y = 4
Step 3: Substitute the value of y into Equation 1:
3x + 6y = 5
3x + 6(4) = 5
3x + 24 = 5
Step 4: Subtract 24 from both sides:
3x + 24 - 24 = 5 - 24
3x = -19
Step 5: Divide both sides by 3:
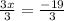
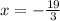
Verify the validity of x and y as solutions:
Verify whether the values for x and y satisfy both equations:

Equation 1: 3x + 6y = 5
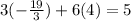
-19 + 24 = 5
5 = 5 (True statement).
Equation 2: -3x - 3y = 7
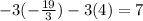
19 - 12 = 7
7 = 7 (True statement).
Therefore, the solutions to the given systems of linear equations are:
 , or
, or
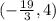 .
.