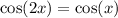
Over the interval [0,2pi), what are the solutions to cos(2x) = cos(x)? check all that apply

Question

asked Apr 22, 2023 63.4k views

1 Answer

Naadira · Answer 1 · 2023-04-27T20:27:40+0000

$\cos(2x) = \cos(x)$

Solution (1)

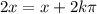
$2x = x + 2k\pi$

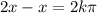
$2x - x = 2k\pi$

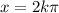
$x = 2k\pi$

for k=0 / for k=1 / for k=-1

x=0 / x=2π / x=-2π

acc / acc / rej

solution (2)

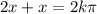
$2x = - x + 2k\pi$

$2x + x = 2k\pi$

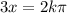
$3x = 2k\pi$

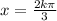
$x = (2k\pi)/(3)$

for k=0 / for k=1 / for k=-1

x=0 / x=2π/3 / x=-2π/3

acc / acc / rej

Note that i'm trying values of K which make the answer belong to our interval;

So our solution which i will represent as a set is;

S € {0,2π/3,2π}