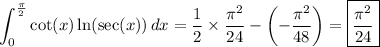Substitute y = tan(x) and dy = sec²(x) dx to transform the integral to
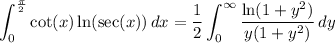
and we split the integral at y = 1.
Examining the one over [0, 1], expand into partial fractions :
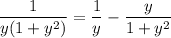
Then
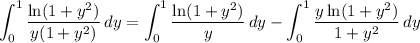
In the integral over [1, ∞), substitute y = 1/z :
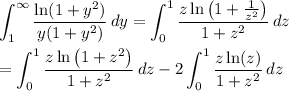
Some terms cancel and we're left with
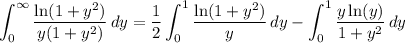
Use the series expansions of ln(1 + y) and 1/(1 - y) - both are valid for |y| < 1.
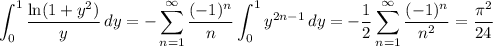
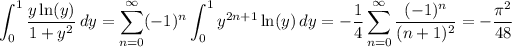
Putting everything together, we have