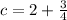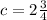Answer:
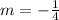
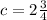
Explanation:
Let's start by finding the point of intersection of the lines x -2y= -1 and y= 2.
x -2y= -1 -----(1)
y= 2 -----(2)
Substitute (2) into (1):
x -2(2)= -1
x -4= -1
x= 4 -1
x= 3
Thus, the point of intersection is (3, 2).
y= 4x +8
Slope= 4
The product of the slopes of perpendicular lines is -1.
4m= -1
m= -¼
y= -¼x +c
Since the line passes through (3, 2), we can substitute this coordinates into the equation to find the value of c.
When x= 3, y= 2,