Question

Evaluate the surface integral. S xz dS S is the boundary of the region enclosed by the cylinder y2 + z2 = 16 and the planes x = 0 and x + y = 10

Answer 1

If you project S onto the (x,y)-plane, it casts a "shadow" corresponding to the trapezoidal region

T = {(x,y) : 0 ≤ x ≤ 10 - y and -4 ≤ y ≤ 4}

Let z = f(x, y) = √(16 - y²) and z = g(x, y) = -√(16 - y²), each referring to one half of the cylinder to either side of the plane z = 0.

The surface element for the "positive" half is

dS = √(1 + (∂f/∂x)² + (∂f/dy)²) dx dy

dS = √(1 + 0 + 4y²/(16 - y²)) dx dy

dS = √((16 + 3y²)/(16 - y²)) dx dy

The the surface integral along this half is

`\displaystyle \iint_T xz \,dS = \int_(-4)^4 \int_0^(10-y) x √(16-y^2) \sqrt{(16+3y^2)/(16-y^2)} \, dx \, dy`

`\displaystyle \iint_T xz \,dS = \int_(-4)^4 \int_0^(10-y) x √(16+3y^2)\, dx \, dy`

`\displaystyle \iint_T xz \,dS = \frac12 \int_(-4)^4 (10-y)^2 √(16+3y^2) \, dy`

`\displaystyle \iint_T xz \,dS = 416\pi`

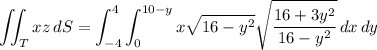
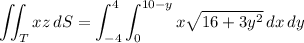
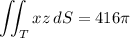
You'll find that the integral over the "negative" half has the same value, but multiplied by -1. Then the overall surface integral is 0.