If you project S onto the (x,y)-plane, it casts a "shadow" corresponding to the trapezoidal region
T = {(x,y) : 0 ≤ x ≤ 10 - y and -4 ≤ y ≤ 4}
Let z = f(x, y) = √(16 - y²) and z = g(x, y) = -√(16 - y²), each referring to one half of the cylinder to either side of the plane z = 0.
The surface element for the "positive" half is
dS = √(1 + (∂f/∂x)² + (∂f/dy)²) dx dy
dS = √(1 + 0 + 4y²/(16 - y²)) dx dy
dS = √((16 + 3y²)/(16 - y²)) dx dy
The the surface integral along this half is
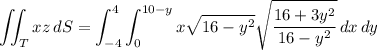
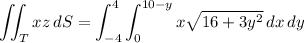
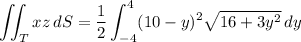
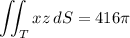
You'll find that the integral over the "negative" half has the same value, but multiplied by -1. Then the overall surface integral is 0.