Answers:
- Slope = undefined; y intercept = none
- Slope = 2; y intercept = -2
- Slope = -1; y intercept = 1
- Slope = 0
- Slope = -4
========================================================
Step-by-step explanation:
1)
For any vertical line, the slope is always undefined. Recall that slope = rise/run. For a vertical line, the run is 0 because there is no left or right movement. This leads to a division by zero error. The vertical line is also parallel to the y axis, meaning that there isn't a y intercept whenever the line isn't directly on top of the y axis.
The equation of this vertical line is x = 3 as all points on this line have the same x coordinate of 3.
-----------------------
2)
We can use the slope formula for the points

So,

The slope is 2.
The y intercept is -2 as this is the location where the diagonal line crosses the y axis.
The equation of this line is y = 2x-2.
-----------------------
3)
Same idea as problem 2.

The slope is -1.
The y intercept is 1 because the line cuts through 1 on the y axis.
The equation is y = -1x+1 which is the same as y = -x+1.
-----------------------
4)
Pick any two points from the table. Each column represents a different (x,y) ordered pair point. Those two points selected are then plugged into the slope formula. I'll pick the first two columns.
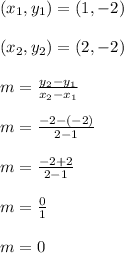
Notice how the y coordinates are the same, which leads to a difference of 0 up top and ultimately the slope itself is also 0. We have a horizontal flat line here. All horizontal lines have a slope of 0.
The y intercept is -2 because all y values for this function are the same.
The equation is y = 0x-2 which is the same as y = -2.
-----------------------
5)
Again I'll pick the first two columns to plug into the slope formula, but you can pick any two columns you prefer.
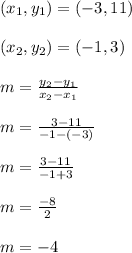
The slope is -4.
Use this slope value, along with any column from the table to form the (x,y) point, to plug into the slope intercept form below. I'll use the first column
y = mx+b
11 = -4*(-3)+b
11 = 12+b
11-12 = b
-1 = b
b = -1
The y intercept is -1.
The equation is y = -4x-1.