Answer:
Approximately
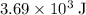 .
.
Step-by-step explanation:
Let
 denote the mass of this cart of bricks and let
denote the mass of this cart of bricks and let
 denote the gravitational acceleration. Let
denote the gravitational acceleration. Let
 denote the constant of kinetic friction between the ground and this cart of bricks.
denote the constant of kinetic friction between the ground and this cart of bricks.
Refer to the diagram attached. There are four forces on this cart of bricks:
- Weight of the cart and the bricks:
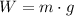 .
. - Normal force from the ground:
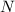 .
. - Friction between the cart and the ground:
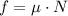 .
. - Force exerted through the rope,
 .
.
Consider the force exerted through the rope in two components:
- Horizontal component of
 :
:
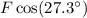 .
. - Vertical component of
 :
:
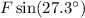 .
.
Since the velocity of this cart is constant, forces on this cart would be balanced. The following would be equal:
- Vertically, the normal force
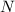 and the vertical component of
and the vertical component of
 should balance the weight of the cart and the bricks:
should balance the weight of the cart and the bricks:
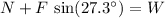 .
. - Horizontally, the horizontal component of
 should balance the friction between the cart of bricks and the ground:
should balance the friction between the cart of bricks and the ground:
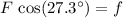 .
.
However,
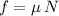 . Thus, the second equation would be equivalent to
. Thus, the second equation would be equivalent to
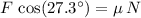 .
.
The weight of this cart of bricks is
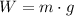 . The first equation would be equivalent to
. The first equation would be equivalent to
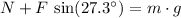 .
.
The value of
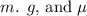 are all given. Thus, these two equations is a system of two equations for two unknowns,
are all given. Thus, these two equations is a system of two equations for two unknowns,
 :
:
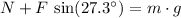 .
.
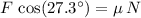 .
.
Solve this system of equations for
 , the size of the force that the rope exerted on the cart or bricks.
, the size of the force that the rope exerted on the cart or bricks.
Rewrite the first equation to find an expression for
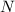 :
:
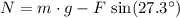 .
.
Substitute this expression into the second equation:
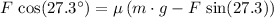 .
.
Rearrange and solve for
 :
:
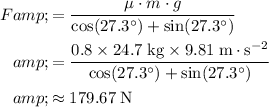 .
.
Thus, the size of the force that the rope exerted on the cart would be approximately
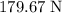 .
.
The floor is horizontal. Thus, the vertical displacement of this cart of bricks would be
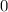 . The vertical component of
. The vertical component of
 would thus have done no work on the cart
would thus have done no work on the cart
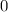 . The entirety of the work that
. The entirety of the work that
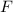 does on this cart of bricks would come from the horizontal component of this force.
does on this cart of bricks would come from the horizontal component of this force.
Given that
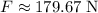 , the horizontal component of this force would be:
, the horizontal component of this force would be:
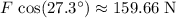 .
.
The horizontal displacement of this cart of bricks is
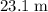 . Accordingly, the work that the horizontal component of
. Accordingly, the work that the horizontal component of
 did on this cart of bricks would be approximately
did on this cart of bricks would be approximately
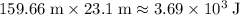 .
.
Thus, the overall work that this rope did on this cart of bricks would be approximately
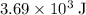 .
.