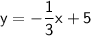Answer:
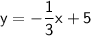
Explanation:
Slope-intercept form of a linear equation:
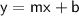
(where m is the slope and b is the y-intercept)
From inspection of the graph, the y-intercept is at (0, 5)
Therefore, b = 5
Choose another point on the line, e.g. (3, 4)
Now use the slope formula to find the slope:
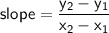
where:
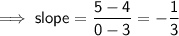
Therefore, the equation of the line is: